Сегодня один из друзей задал мне вот такую задачу:
Эта задача, как и все подобного рода, может не иметь одного точного ответа. При её решении скорее важен процесс, ход мысли, чем сам результат.
Разберём подробней условие задачи.
С одной стороны опущены существенные факторы, с другой - присутствует излишняя конкретика.
Поэтому нам придется ввести некоторые допущения и дополнения, обусловленные желанием привести задачу к реальной жизни.
Итак:
Из аналогий становится понятно, что качественное решение задачи выглядит следующим образом. Цена курицы для случаев:
У тебя есть курица, она один раз в год несет одно золотое яйцо. Это яйцо можно продать за 100 долларов, цена всегда постоянная. Курица живет вечно и не болеет)) вопрос, за сколько продать курицу и почему за эту цену?Что же попробуем её решить.
Эта задача, как и все подобного рода, может не иметь одного точного ответа. При её решении скорее важен процесс, ход мысли, чем сам результат.
Разберём подробней условие задачи.
С одной стороны опущены существенные факторы, с другой - присутствует излишняя конкретика.
Поэтому нам придется ввести некоторые допущения и дополнения, обусловленные желанием привести задачу к реальной жизни.
Итак:
- С ходу выкидываем слово «золотое». Вряд ли автор задачи хотел от нас расчёта веса яйца, исходя из текущих котировок золота, а также построения прогнозов изменения цен драг. металлов во времени. Хотя и это при желании мы могли бы сделать.
- «Курица живет вечно и не болеет», позволяет допустить нам, что расходы на содержание курицы на промежутке времени в бесконечность равны нулю.
- Будем считать, что на момент продажи курица уже снесла одно яйцо, которое продажи не подлежит и следующее такое яйцо появится не ранее, чем через год. Т.о. мы сможем использовать классические формулы постнумерандо.
- Яйца не представляют какой-либо художественной, культурной или исторической ценности ни сейчас, ни в будущем. А значит нам не придётся строить различные аукционные модели цены.
- Чтобы не растягивать статью, предположим, что полученные от реализации одного яйца $100 не реинвестируются нами. Покупатель полученные от курицы доходы также собирается сразу тратить. Дополнить расчёт с учетом реинвестирования предлагается читателю в качестве домашнего задания.
- Вложения в курицу обладают абсолютной «безрисковостью». Для всех остальных видов инвестирования: в депозит, облигации правительства и т.д. риск отличен от нуля.
- Ценность получения дохода наследниками, как для покупателя, так и для продавца равна ценности получения дохода лично для себя. Поэтому мы можем использовать для сроков меньше и больше человеческой жизни одни и те же модели. А время приравнивать к бесконечности.
Вопрос учета инфляции и стоимости яйца выделим в отдельно. И постараемся привести решения для двух случаев:
- Инфляция учитывается, номинальная стоимость яйца постоянная.
В жизни это означает, что фактор перепроизводства указанных яиц в стране уменьшает их ценность ровно на величину инфляции. - Инфляция не учитывается, реальная стоимость (или ценность) яйца постоянная.
В жизни это означает, что номинальная стоимость яйца изменяется с темпом, равным инфляции в стране.
Возможен вариант и с долгосрочной облигацией надежного заёмщика. До недавнего времени в качестве примера можно было привести 30-ти летние U.S. Treasure Bonds.
При допущении B видна аналогия с продажей розничного бизнеса. Когда с ростом инфляции, растёт и выручка компании, а значит и личный доход собственников. При этом указанный доход равен стоимости одного и того же количества потребительских корзин.
Из аналогий становится понятно, что качественное решение задачи выглядит следующим образом. Цена курицы для случаев:
- равна сумме долгосрочного депозита, со схожими процентными платежами или стоимости долгосрочной, а лучше вообще бессрочной, облигации со схожим купоном.
- равна стоимости привилегированной акции универсального ритейлера с фиксированным дивидендом (в % от выручки).
Для количественного решения придется вспомнить об аннуитетах и дисконтированной стоимости.
В данном случае нам понадобится бессрочный аннуитет - перпетуитет. Сумма платежей по перпетуитету вычисляется по формуле:
где CF - аннуитетный платеж, i - ставка инфляции, PV - сумма всех приведённых аннуитетный платежей.
Эту формулу ещё называют формулой бессрочной ренты.
Задавшись величиной текущей инфляции, можно определить цену курицы. Так, например, для инфляции в 7% её цена составит $1429. Дисконт для покупателя заложен в том факте, что в большинстве экономик мира ставка по депозитам меньше величины инфляции. И это не считая ненулевого риска самого депозита. Но об этом чуть ниже.
Таким образом, для создания схожего денежного потока, покупателю придется потратить бОльшую сумму, т.е. заплатить бОльшую цену. Разница этих цен зависит как от абсолютных, так и от относительных значений ставок. Ниже приводится таблица разниц цен.
Таким образом, для создания схожего денежного потока, покупателю придется потратить бОльшую сумму, т.е. заплатить бОльшую цену. Разница этих цен зависит как от абсолютных, так и от относительных значений ставок. Ниже приводится таблица разниц цен.
| Инфляция | Депозит | Разница цен |
|---|---|---|
| 10% | 9% | $111.11 |
| 10% | 5% | $1000.00 |
| 7% | 6% | $238.10 |
| 7% | 3% | $1904.76 |
Как видно из таблицы, в некоторых экономических ситуациях курицу можно продавать даже с премией к цене.
Для случая B мы уже не можем использовать использовать формулу бессрочной ренты, т.к. в этом случае знаменатель у нас равен нулю.
Поэтому опорной ценой у нас уже будет сумма депозита, генерирующего сходный денежный поток. А дисконт для покупателя будет заложен в разнице рисков между депозитом (или займом) и «абсолютной» надежностью вложений в курицу. Ведь даже самый надежный инструмент обладает ненулевой мерой риска. А любая ненулевая вероятность потерь на бесконечности превращается в единицу. При сравнении с «безрисковым» вложением со ставкой 3%, цена курицы составит $3333.33
В конце статьи хотелось бы ещё раз затронуть допущение №7. Напомню, что оно определяет одинаковую ценность всех платежей для субъекта независимо от того будет он жив на тот момент или нет.
Как подсказывает психология, в большинстве случаев это не соответствует действительности.
Наверняка, Вы и сами во время чтения задачи прикидывали в уме, какой мультипликатор взять 5-10-15 лет. И это естественно для человека, принимающего решения, которое затрагивает лично его.
Таким образом для случае продажи курицы, несущей ценные яйца физическим лицом, следует это допущение убрать. Это обстоятельство, во-первых, заставляет нас отказаться от бесконечности платежей, а значит от формулы бессрочной ренты, и вернутся к классической формуле дисконтирования денежных поток. А, во-вторых, ввести коэффициент, учитывающий ценность будущих платежей для субъекта-покупателя и продавца с учетом их возраста и социо-демографических характеристик.
Изобретать велосипед не нужно, такой коэффициент уже ввёл Валерий Галасюк, академик АЭН Украины, и назвал своим именем в рамках антропологической концепции дисконтирования (GAD-сonception – Galasyuk’s anthropological discounting conception). Указанный коэффициент рассчитывается по методике, использующей статистические данные о смертности и продолжительности жизни. Что, как вы понимаете, не синонимично. Но это уже тема отдельной статьи.
Как видите, на примере простенькой задачки, нам удалось окунуться в проблематику оценки инвестиционных проектов и принятии финансовых решений. Надеюсь Вам было интересно.
Для случая B мы уже не можем использовать использовать формулу бессрочной ренты, т.к. в этом случае знаменатель у нас равен нулю.
Поэтому опорной ценой у нас уже будет сумма депозита, генерирующего сходный денежный поток. А дисконт для покупателя будет заложен в разнице рисков между депозитом (или займом) и «абсолютной» надежностью вложений в курицу. Ведь даже самый надежный инструмент обладает ненулевой мерой риска. А любая ненулевая вероятность потерь на бесконечности превращается в единицу. При сравнении с «безрисковым» вложением со ставкой 3%, цена курицы составит $3333.33
В конце статьи хотелось бы ещё раз затронуть допущение №7. Напомню, что оно определяет одинаковую ценность всех платежей для субъекта независимо от того будет он жив на тот момент или нет.
Как подсказывает психология, в большинстве случаев это не соответствует действительности.
Наверняка, Вы и сами во время чтения задачи прикидывали в уме, какой мультипликатор взять 5-10-15 лет. И это естественно для человека, принимающего решения, которое затрагивает лично его.
Таким образом для случае продажи курицы, несущей ценные яйца физическим лицом, следует это допущение убрать. Это обстоятельство, во-первых, заставляет нас отказаться от бесконечности платежей, а значит от формулы бессрочной ренты, и вернутся к классической формуле дисконтирования денежных поток. А, во-вторых, ввести коэффициент, учитывающий ценность будущих платежей для субъекта-покупателя и продавца с учетом их возраста и социо-демографических характеристик.
Изобретать велосипед не нужно, такой коэффициент уже ввёл Валерий Галасюк, академик АЭН Украины, и назвал своим именем в рамках антропологической концепции дисконтирования (GAD-сonception – Galasyuk’s anthropological discounting conception). Указанный коэффициент рассчитывается по методике, использующей статистические данные о смертности и продолжительности жизни. Что, как вы понимаете, не синонимично. Но это уже тема отдельной статьи.
Как видите, на примере простенькой задачки, нам удалось окунуться в проблематику оценки инвестиционных проектов и принятии финансовых решений. Надеюсь Вам было интересно.
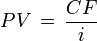
Комментариев нет:
Отправить комментарий